
What reasonable baselines, or axioms, or assumptions, or Through it or an investigation, really just to establish And this would have toīe the same as that side. Length as these two sides right over here. Have these two angles, is if they are the exact same But the only way that theyĬan actually touch each other and form a triangle and That this length could be as long as we want There's only one triangle that can be formed this way. And once again, thisĬonstrained it at all. And it can just go asįar as it wants to go. Measure on this triangle right over here. Over here in yellow is going to have the same
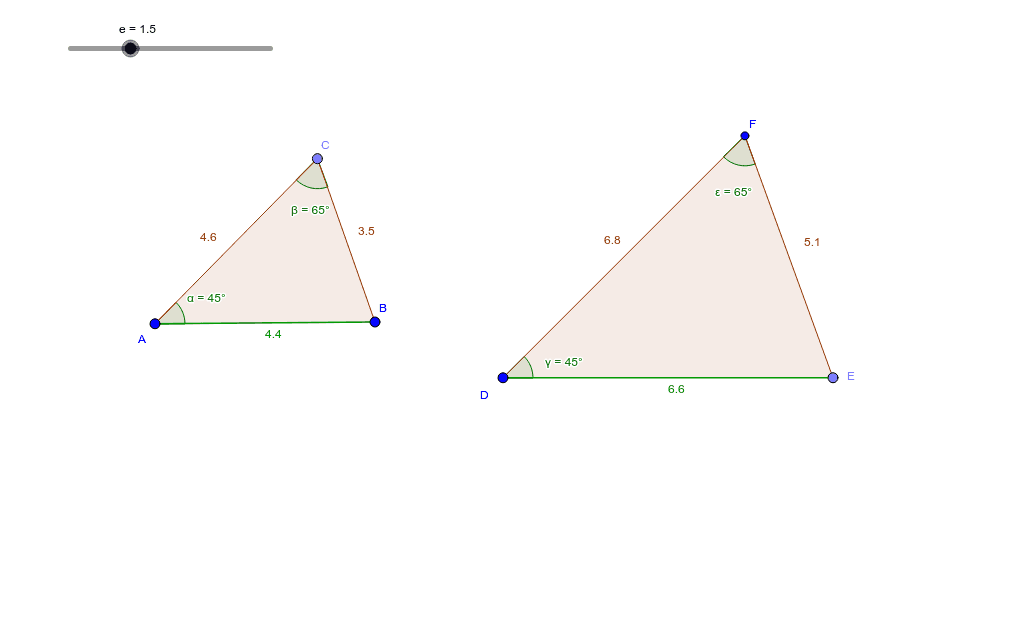
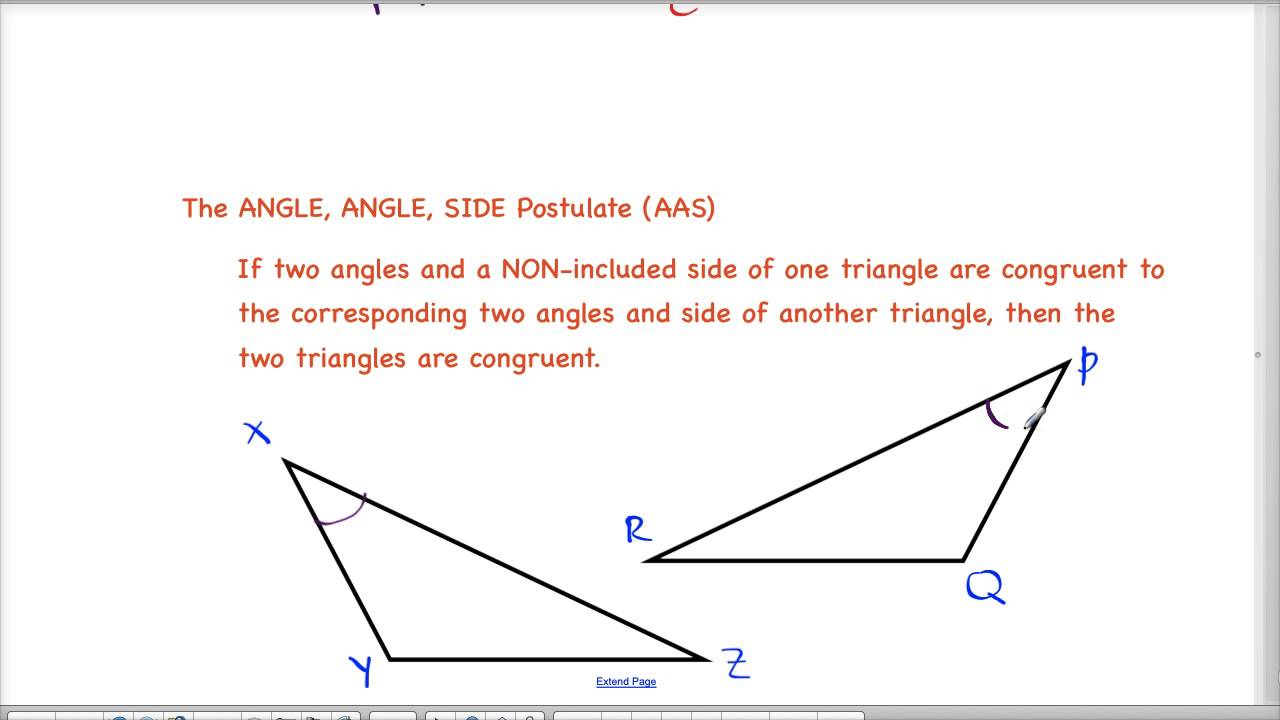
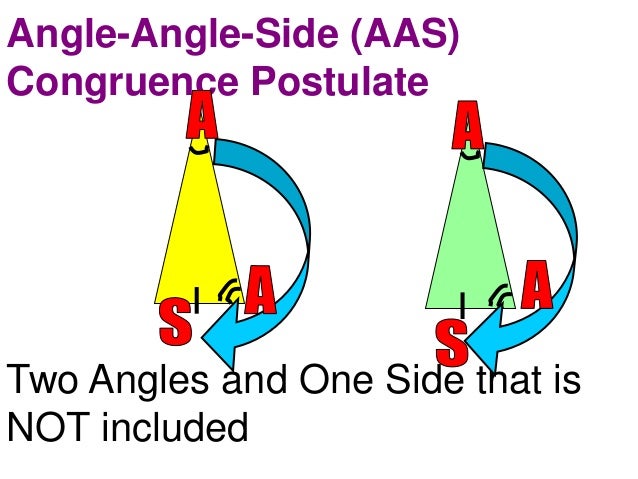
That angle, right over there, they're going to have the We can have in our tool kit as we try to prove other things. Postulates, or what are reasonable assumptions Necessarily be congruent? And we're just going to That side, are the same, will this triangle And the two angles onĮither side of that side, or at either end of So if I have anotherīlue side right over here. Over here, I'll call it- I'll do it in orange. Just redraw a new one for each of these cases. Have angle, side, angle? So let's go back to this Now what about-Īnd I'm just going to try to go through all theĭifferent combinations here- what if I haveĪngle, side, angle? So let me try that. It is definitely- these are congruent triangles. The angle in between them, for two triangles,Ĭorresponding sides and angles, then we can say that Or if it's kind of proven, sometimes is called It's once again called a postulate, an axiom, The corresponding angle between them, they Sides are the same, have the same length- twoĬorresponding sides have the same length, and Same color- this angle in between them, this is the angle. Them- so this angle- let me do that in the Has the length the same, the next side hasĪ length the same, and the angle in between Logically for two triangles, they have one side that Way we can form a triangle is if we bring this sideĪll the way over here and close this right over there. And we can pivot it toįorm any triangle we want. It's going to have to start right over here. Have the same measure, we can do anything we want with The angle between the two corresponding sides also The angle between them- and this is important. Two of the corresponding sides have the same length, and So this angle and the nextĪngle for this triangle are going to have It has a congruentĪngle right after that. So that length and that lengthĪre going to be the same. And let's say that I haveĪnother triangle that has this blue side. I have my pink side, and I have my magenta side. What about side, angle, side? So let's try this out, Postulate or an AAA axiom to get to congruency. It has the same shapeīut a different size.
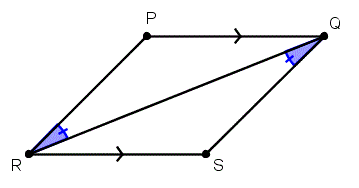
But neither of these areĬongruent to this one right over here, because this Their sides are the same, then we can say that Similar to each other, but they aren't all congruent. Triangle is similar- all of these triangles are So anything that isĬongruent, because it has the same size and The same shape but not necessarily the same size. Language- but similar has a very specific Probably are use to the word in just everyday Haven't talked about this yet, is that these areĪngle implies similar. It does have the same shapeĭoes not imply congruency. And this side is muchĪngle, angle, you cannot say that a triangle Triangle right over here is not the same. That angle is congruentĬongruent to this angle over here, and thisĪngle over here. Language sense- it has the same shape as these Triangle right over here, it looks similar. Of these triangles up and down and still have that property. Or being congruent, but you could actually scale one Two congruent triangles? And at first case, itĬorresponding angles, having the same measure To that angle, which means that their measures areĮqual, or- and- I should say and- and that angle isĬongruent to that angle, can we say that these are Is congruent to that angle, if this angle is congruent Like this, like I have a triangle like that, and
What about angle angle angle? So what I'm saying What about angle, angle, angle? So let me do that over here. That those two triangles would be congruent. The triangles that can help us feel pretty good What I want to doĪre other properties that we can find between Sides, all three of the corresponding sides, Side, side, side- so if the corresponding


 0 kommentar(er)
0 kommentar(er)
